What is maths? They say its the basics of all fundamentals which we humans learnt...how to count and keep everything in order. And then what are relation... again i guess right from adam and eve humans learnt its meaning. The two terms got mixed and we got "Mathematical Relations".
Right form childhood we have heard this term "mathematical relation". Many of my friends used to hate maths when i used to score 100 in primary classes. They used to say maths is tough.. I used to say maths is the easiest. Time passed, Math really grew tough and so do the relations.. I used to always try and explain maths.. and relations.. to people. Always felt too sure, too confident about these two things in my life that i can never get wrong here. I know them correctly. But nopes. Things were never that simple.
What went wrong?
Law of associativity - a + ( b + c ) = ( a + b ) + c
Simple enough! But mathematically! It does not hold at all when it comes to relations. With the passage of time, in a group of three people, 2 will come closer..share secrets..talk..and yes third is still there. To an outsider, it is all same.. but internally it is not. The whole summation of the group has changed by putting those brackets around two. And if the same bracket is with other combination of 2 in the group.. again it changes.
End Result - a + ( b + c ) ≠ ( a + b ) + c and infact the best thing for this relation is leaving it as a + b + c only!
Law of distributivity - a * ( b + c ) = a*b + a*c
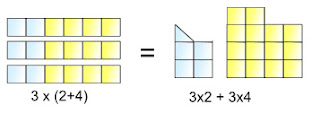
This is much more easier to understand. Again mathematically it is very simple. But take it from relation point of view. In a group of two if third person enters.. do you think that this third person distributes/shares his time, emotions, problems, secrets and all this equally?? No right! in some cases, 'b' is more close to 'a' and in other 'c' .. that is mathematically speaking.. value of 'a' differs as soon as the bracket is open! It is not the same person any more. Rather you can say it becomes a1 and a2 making the value of the relation different than intended.
Therefore, it is always better for 'b' and 'c' to tackle 'a' from inside the bracket i.e. not opening themselves individually to this outsider.
And adding on to these.. I just felt that it is not just maths but other subjects which defines relations. Take thermodynamics. Zeroth law of thermodynamics state that if a is equal to b and b is equal to c then a is bound to be equal to c. Writing mathematically - If a = b & b = c then a = c
Give it a thought..hardly you see this happening! 'a' is a very good friend of 'b' and 'b' is a very good friend of 'c. But then it is not a confirmation that 'a' should be a good friend of 'c'. In fact 'a' and 'c' could be arch rivals or non existent for each other. And from the point of expectation of 'b' also it is not justified at all to think that 'a' and 'c' should be as good together as they are with him.
Only thing which i think is holding true is Newton's first law, a body in motion will remain in motion and a body at rest will remain at rest unless it is acted upon by external force.
A relation will remain in tact unless there is an outside force which tries to disrupt it. Any external news, gossip, person, truth, lie, anything will alter this state of trust, equilibrium and harmony - however minutely or largely it do.

